What is the Two Generals’ Problem?
The Two Generals’ Problem, also known as the Two Generals’ Paradox or the Two Armies Problem, is a classic computer science and computer communication thought experiment that we’re going to talk about in this post.
First of all, to avoid any confusion, we need to remember that the Two Generals’ Problem, although related to the Byzantine Generals’ Problem is not the same. Byzantine Generals’ Problem is a more general version of the Two Generals’ Problem and it’s often discussed when talking about distributed systems, fault tolerance and blockchain. We’ll be talking about it in the following post.
But now let’s move to the story of the two generals.
The story of the Two Generals

Let’s imagine two armies, led by two generals, planning an attack on a common enemy. The enemy’s city is in a valley and has a strong defence that can easily fight off a single army. The two generals have to communicate with each other to plan a synchronised attack as this is their only chance to win. The only problem is that to communicate with each other they have to send a messenger across the enemy’s territory. If a messenger is captured the message he’s carrying is lost. Also, each general wants to know that the other general knows when to attack. Otherwise, a general wouldn’t be sure if he’s attacking alone and as we know attacking alone is rather pointless.
Now, let’s go through a simple scenario. Let’s call our generals A and B and let’s assume everything goes perfectly fine. General A, who is the leader, sends a message – “Attack tomorrow at dawn”. General B receives a message and sends back an acknowledgement – “I confirm, attack tomorrow at dawn”. A receives B’s confirmation. Is this enough to form a consensus between the generals? Unfortunately not, as General B still doesn’t know if his confirmation was received by General A. Ok, so what if General A confirms General’s B confirmation? Then, of course, that confirmation has to be also confirmed and we end up with an infinite exchange of confirmations.
In the second scenario, let’s also assume that General A sends a message to General B. Some time has passed and General A starts wondering what happened to his message as there is no confirmation coming back from General B. There are two possibilities here. Either the messenger sent by General A has been captured and hasn’t delivered a message or maybe B’s messenger carrying B’s confirmation has been captured. In both scenarios, they cannot come to a consensus again as A is not able to tell if his message was lost or if it was B’s confirmation that didn’t get through. Again, we ended up in an inconsistent state which would result in either General A or B attacking by himself.
We can quickly realise that no matter how many different scenarios we try and how many messages we send we cannot guarantee that consensus is reached and each general is certain that his ally will attack at the same time. To make it even worse, there is no solution to the Two Generals’ Problem, so the problem remains unsolvable.
I hope you can clearly see an analogy to computers’ communication here.
How is this related to computer science and TCP?
Instead of two generals, let’s imagine two computer systems talking to each other. The main problem here is again the untrusted communication channel and inconsistent state between two machines. A very common example that always comes up when talking about the Two Generals’ Problem is the TCP protocol.
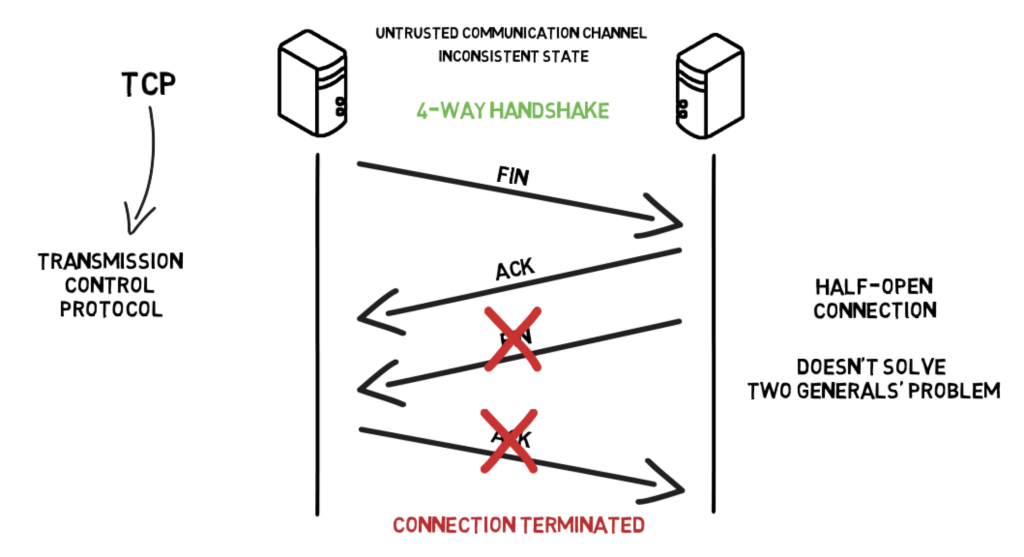
As we probably know, TCP uses a mechanism called 4-way handshake to terminate the connection. In this mechanism, a system that wants to terminate a connection sends a FIN message. The system on the other side of the communication channel replies with an ACK and sends its own FIN message which is followed by another ACK from the system which initialised termination. When all of those messages are received correctly, both sides know that the connection is terminated. So far it looks ok, but the problem here is again the shared knowledge between the two systems. When, for example, the second FIN is lost we end up with a half-open connection where one side is not aware that the connection has been closed. That’s why even though TCP is very reliable protocol it doesn’t solve the Two Generals’ Problem.
So maybe a pragmatic approach?
I’m happy you’re not giving up. Unsurprisingly, there was a number of people trying to solve unsolvable Two General’s Problem and they came up with a few practical approaches. The main assumption here is to accept the uncertainty of the communication channel and mitigate it to a sufficient degree.
Let’s go back to our generals. What if General A instead of sending only 1 messenger sends 100 of them assuming that General B will receive at least 1 message. How about marking each message with a serial number starting from 1 up to 100. General B, based on the missing numbers in the sequence, would be able to gauge how reliable the communication channel is and reply with an appropriate number of confirmations. These approaches, even though, quite expensive are helping the generals to build up their confidence and come to a consensus.
If sacrificing messengers is a problem, we can come up with yet another approach where the absence of the messengers would build up generals’ confidence. Let’s assume that it takes 20 minutes to cross the valley, deliver a message and come back. General A starts sending messengers every 20 minutes until he gets a confirmation from General B. Whenever confirmation arrives General A stops sending messengers. In the meantime, General B after sending his messenger with his confirmation awaits for the other messengers coming from General A, but this time an absence of a messenger builds up General’s B confidence as this is what the Generals agreed on.
In this case, we have a clear speed vs cost tradeoff and it’s up to us which approach is more suitable to our problem.
That’s the end of the story of the Two Generals. Time for a quick summary.
Summary
Two Generals’ Problem is a classic computer science problem that remains unsolvable.
It comes up whenever we talk about communication over an unreliable channel.
The main problem is an inconsistent state caused by lack of common knowledge
There are some pragmatic approaches to the Two Generals’ Problem.
Extras
Two Generals’ Problem was first published in 1975 in “Some Constraints and Trade-offs in the Design of Network Communications” paper and described a problem with communication between two groups of gangsters. If you want to read the original version check this link.



